前回の記事では薬物の分布容積について学んだことを書きました。 今回は薬物の投与から消失までをコンパートメントモデルに当てはめて考えてみたいと思います。
コンパートメントモデルとは?
コンパートメントとは、仕切られた区画のことです。
コンパートメントモデルとは、ヒトの体を四角い箱に例えて、薬物の投与量と消失を考えるモデルです。
薬物は皮膚や粘膜から吸収される、または直接静脈内に投与することで全身を循環する血液に入ります。
ヒトの体を血液が入った1つの入れ物として考える場合、1-コンパートメントモデルといいます。
また、薬物の組織移行性を考慮して、2つの入れ物として考える場合を2-コンパートメントモデルといいます。
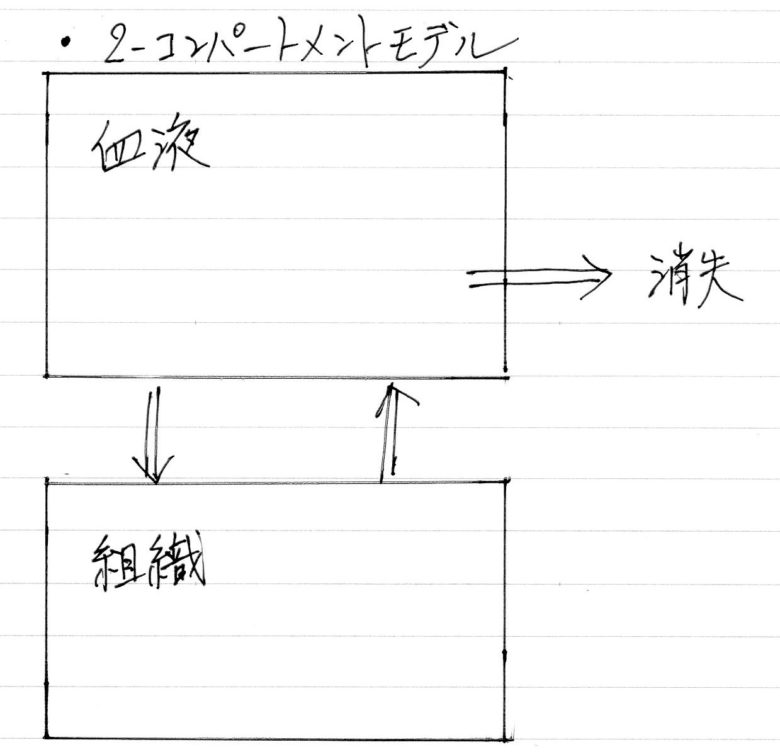
薬物の消失と時間の関係
1-コンパートメントモデルでは、投与された薬物が体循環血に入ると直ちに全体に分布して均一な濃度になると仮定します。
血液中の薬物はその後代謝を受け、排泄されて体内から消失します。
静脈内投与の場合、投与直後の血中濃度が最大となり、時間の経過と共に濃度は低下します。
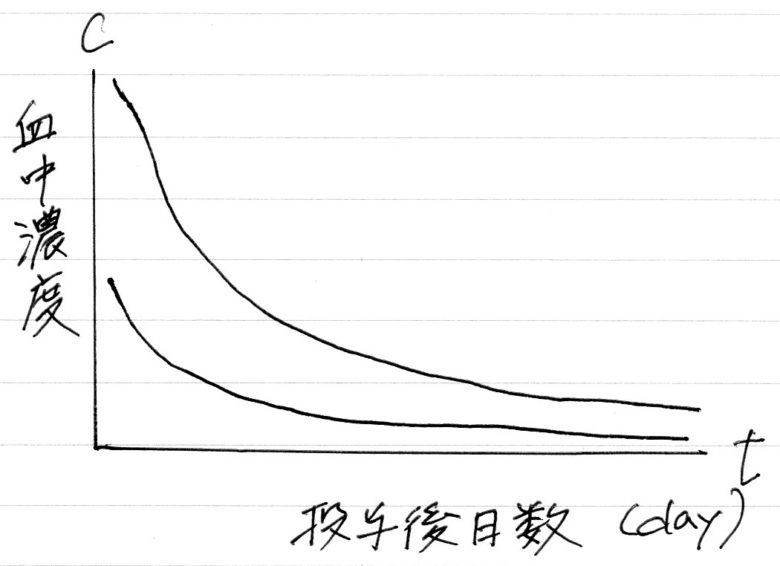
血液というコンパートメントから薬物が出て行く(消失する)速さの程度を表すのが「消失速度定数」。この消失速度定数が、薬物の消失半減期に関係してきます。
血液からの薬物の消失を式で表すと、
-dC/dt=keC
となります。
Cは血中濃度、tは時間、keは消失速度定数で、dはわずかな変化を意味しています。
つまり、dC/dtは、すこしだけ時間が経過したときの血中薬物濃度の変化を表し、薬物量は減少していくため-(マイナス)となっています。
コンパートメントモデルに当てはめるとこのようになります。
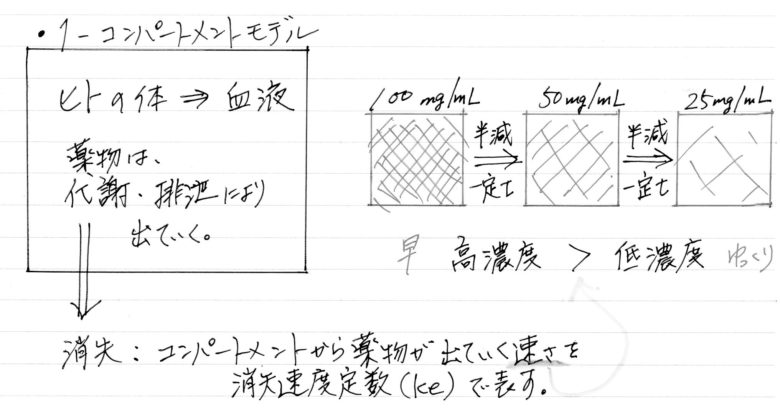
血中濃度が半減するまでにかかる時間は一定であるため、薬物は血中濃度が高いときは早く消失し、血中濃度が低くなるとゆっくり消失します。
添付文書をみてみよう
ハーセプチンの添付文書によると、トラスツズマブとして1~8mg/kgを90分間点滴静注(単回投与)したときの血清中濃度と半減期は以下のとおり(数値はmean)。
このときの半減期は1-コンパートメントモデルを当てはめて算出したと記載されています。
- 1mg/kg → Cmax:19 μg/mL、t1/2:2.4日
- 2mg/kg → Cmax:43 μg/mL、t1/2:2.6日
- 4mg/kg → Cmax:72 μg/mL、t1/2:5.9日
- 8mg/ kg → Cmax:177 μg/mL、t1/2:5.5日
半減期を用いてざっくり計算してみると、投与後21日目の血中濃度は、
- 1mg/kg → ほぼ0に近い
- 4mg/kg → 約13 μg/mL
- 8mg/kg → 約22 μg/mL
となり、添付文書に記載のグラフからもおおよそこのくらいの数値であることが読み取れます。
消失速度がゆるやかであることから、トラスツズマブの消失速度定数は小さいことが想像されます。
参考図書
今回、添付文書に登場したキーワードをヒントに薬物動態の勉強を始めましたが、こちらの本が大変わかりやすく役に立ちました。
この本の冒頭に、薬物動態は学ぶものではなく使うもの、と書かれているのですが、すこし勉強しただけでもそのとおりだと感じています。
私の場合は、翻訳という仕事に必要な範囲・レベルの知識を得ることが目的です。
まずはこの本を足がかりにしてすこしずつ深掘りし、肉付けしながら理解を深めたいと思います。



コメント